The past two weeks have seen me chained to my computer. No new samples to process. I did get out thru the office door to passage my cells, once a week, as usual, and I helped Jenny Olins, a student in Sam Hazen’s lab, do polarizing light microscopy for an hour or so. But mostly it was writing and calculating. Paper writing is a good thing. I have considered for these accounts to write about writing. It something I do in the week. But for the meantime I am keeping that off limits, wanting to blog about the experimental side of my life. But calculating is part of the doing of science. A computer is an instrument like any other. Sometimes looking through a microscope is enough. But most of the time it isn’t: looking has to be enhanced by measurements and calculations.
When I started these posts, Lab Fab Season 1, I was working (on sabbatical at Nottingham) on root growth, a problem that occupied many blog entries. Likewise root growth shows up in the first few posts of season two (e.g., here), about a year ago. Then it slips from view, not because nothing was doing, but because it wasn’t me doing it. Experiments were being run by my trusty assistant, Ellen Zelinsky. Doesn’t seem right to blog about someone else’s work in the lab, even if I am supervising.
But this past week, I got my hands back in the root growth and oscillation game, at least on the computer. To have any chance of making sense, I have to provide a wee bit of introduction. It would be too rude to link to a few dozen earlier posts and say read ‘em. Tho—if you are really keen… (links above).
As difficult to see as roots are in the garden, they are easy to see in the laboratory. A small plant like arabidopsis is typically grown on a Petri dish, on agar medium, as it were a giant bacterium (Fig. 1). As for scale, the square Petri dish has sides of about 10 cm. The agar is transparent and the root grows along the surface. To be sure, the roots of some species are disturbed by light, but not this one. In this example, I had scratched the back of plate with a razor (the scratches are the short horizontal lines) where the root tip was, once per day. The distance between the scratches, along the line of the root, record the distance travelled by the root tip each day, which generally what is meant by ‘root growth’.
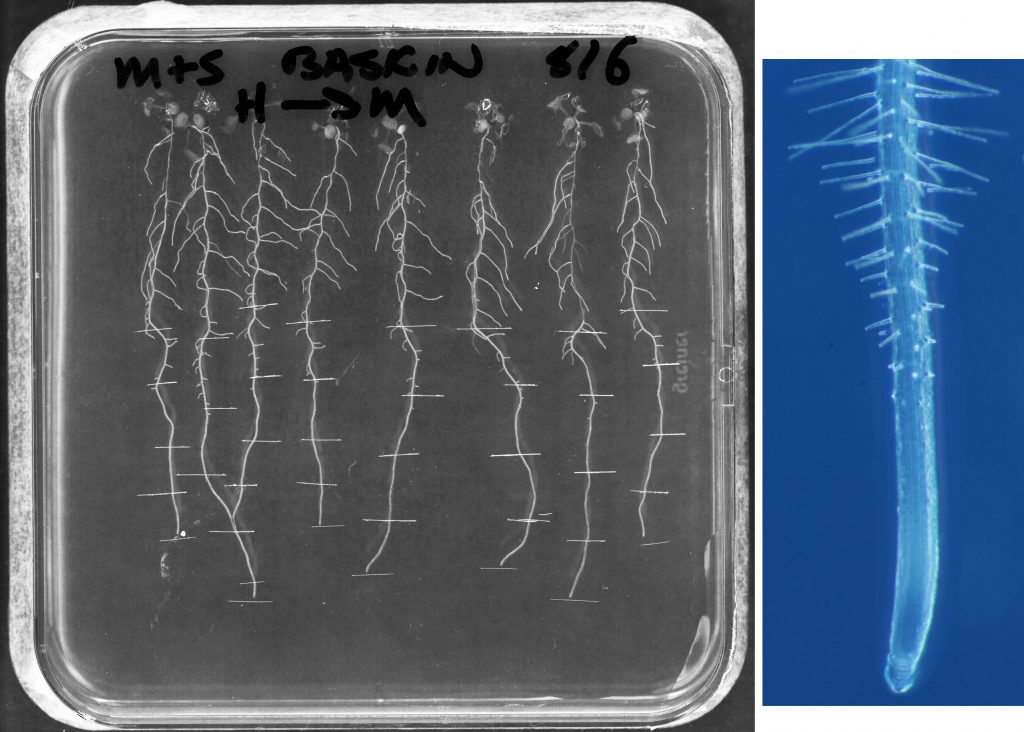
To get a better look at the root, I can place the whole Petri dish on a microscope. The color photograph shows the root tip, taken thru a microscope. Again, for scale, the diameter of the arabidopsis root is a bit more than 0.1 mm. That is correct, only a bit more than 1/10 of a millimeter. That’s pretty thin! The picture shows the region of the root where growth occurs, the root tip. At the very tip of the root is a region called the ‘meristem’, where cells are small, elongate slowly, and divide. The meristem takes up about 0.4 mm of the growth zone. After that, cells stop dividing and elongate rapidly. This region of rapid elongation takes up about 1 mm. Then, elongation stops and cells mature. The place where elongation stops is about where the hairs become obvious. Yes, those things that look like hairs are called, in a bit of nomenclatural panache, root hairs.
The salient point about the root growth zone, from the perspective of the research that I am doing, is that it comprises a zone (the meristem) where growth is slow, and another zone (rapid elongation zone) where growth is fast. How is the transition between those different regimes managed? The difference in growth rate is about a factor of ten. It is not entirely obvious how cells can move smoothly from one regime to the other.
To investigate, I took the approach of imaging a growing root for three hours and looking at the stability of the growth pattern in both zones. Turns out to be really stable. No obvious monkey business whatsoever. Still, with rigorous analysis, made possible by help from a mathematician at University of Nottingham called Simon Preston, we discovered that the pattern of growth oscillates. That sounds vague – the pattern of growth? It is vague because the rigorous analysis in question is called ‘Principal Component analysis’, a mathematical technique where the entire data set is turned into a vast, N-dimensional object (in this case, N = 37 x 2400) and axes are found, piercing the object, around which most of the data vary. If that doesn’t make much sense, it is because I don’t understand it fully myself. But the gist is that the Principal Components capture mathematically large features of the data.
What we found is that the first Principal Component, the biggest, one that explains more than half of the variation in the entire data set, oscillates over time. You can see a plot here. Strictly speaking, I should call it a fluctuation not an oscillation because I don’t know how regular in time the changes are, although for the twelve roots analyzed in Nottingham, the fluctuation in Principal Component 1 looks reasonably sinusoidal. The period is about 90 min.
Finding a pattern is inherently interesting; the frustrating bit is that the pattern is represented by an abstract mathematical object (a Principal Component). What is oscillating, really? I mean what concrete property of the root? To find that out, I have been asking with what is this Component correlated. An obvious choice is the average rate of elongation, remembering that there are two such average rates, one for the meristem and the other for the zone of elongation. Here is an example of such a search for correlation where Principal Component 1 is plotted on the x-axis and elongation rate of the zone of rapid elongation is plotted on the y-axis (Fig. 2).
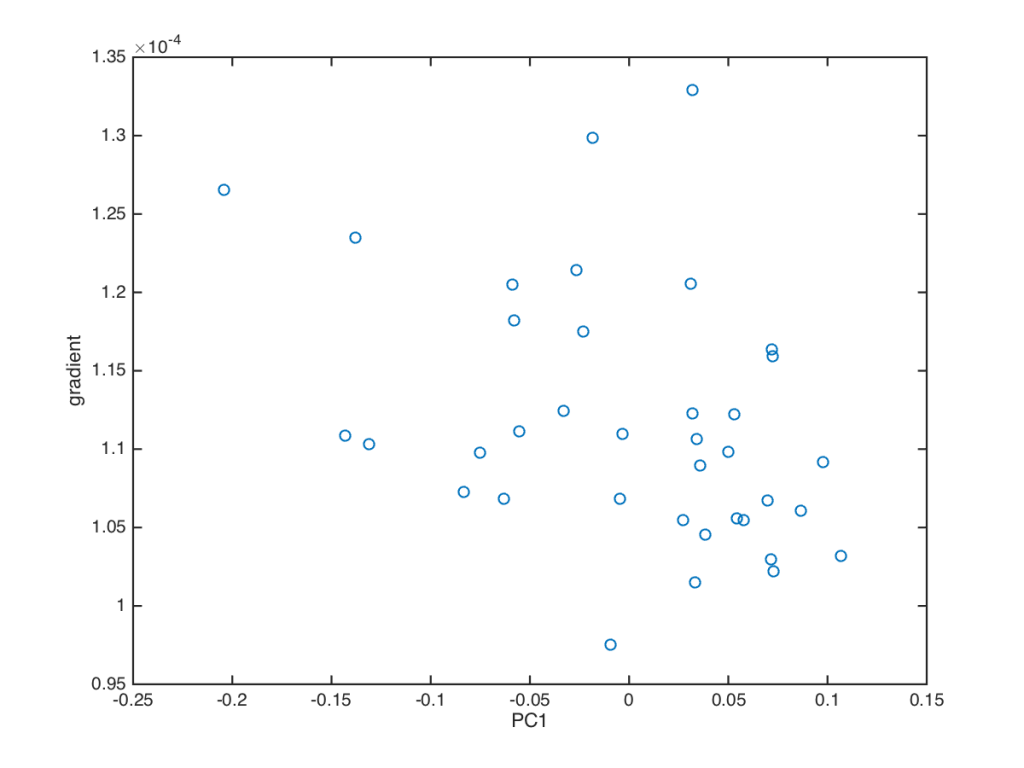
Well if I squint at this I can see a little bit of a trend in the data but nothing too exciting, correlation wise. Not shown are many of the other roots where the plot looks like my dart throwing–completely random.
But this past week, Simon sent me a little bit of code to help check a different correlation. This one looks at, essentially, the position where rapid elongation starts. That is, I chose a particular value representing growth rate and said when a cell hits this value, hey presto!, it has gained the status of rapid elongation. Then the question becomes, does the position oscillate where growth rate attains that value? The question is equivalent to asking: Does the position where the zone of rapid elongation begins move back and forth toward the root tip? Simon’s code plots this position versus Principal Component 1. Here is an example (Fig. 3):
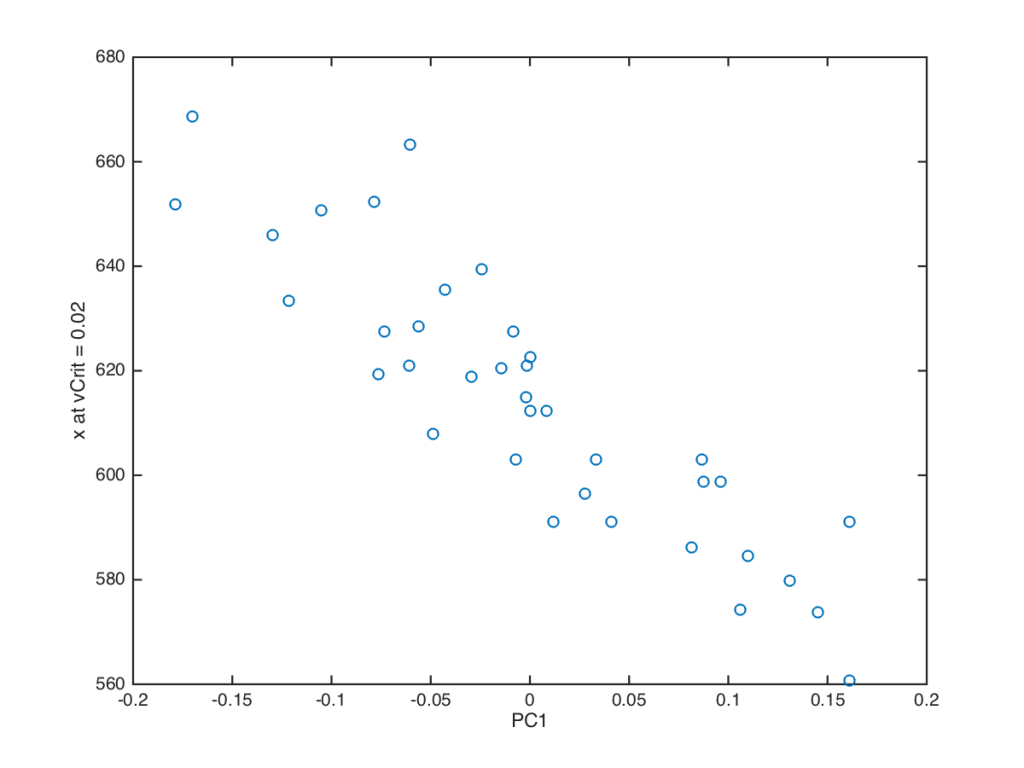
Now that looks like a correlation! And among the 12 of the roots in the data set, two are loose, tho not as loose as that of Fig. 2, and the other ten are as tight as Fig. 3. This smells like a finding. Whatever is responsible for allowing a zone of slow growth (the meristem) to sit beside a zone of fast growth (the rapid elongation zone) admits of some back and forth in position of the boundary.
Now, I need to see if I can see the same thing for the roots imaged at UMass. This is what Ellen has been helping with and we are experiencing … technical difficulties. To be described anon.
When I measured the rate of tip-growth in Vaucheria in response to a
second of blue light pulse, I found the alga’s growth showed oscillation with a period of 4-5 min. But I met a difficulties in measuring the increment of the growth at an interval of 3 min with microscope. The oscillation might be artificial. If i measured the position of the cell apex a little bit larger than the true position, the next increment would be a little bit shorter than the real value. That is, the oscillation could be due to human resolution of the sight..
By repeated measurement, however, this possibility must first be taken into account when the growth rate was below 1 micrometer/ min. Vaucheria exhibit positive light-growth response to Blue Light pulse. The growth rate oscillated with a period of 5 min. So, shining BL pulse every 5 min, Vaucheria showed drastic oscillation by resonance to the incident pulses. Your experiment seems very interesting to know where the origin of the oscillation. It seems to be arosen from the quiescent center.