Non-equilibrium Quantum Dynamics and Transport
The study of closed quantum systems out-of-equilibrium, with or without disorder, opens the door to new and exciting conceptual questions about dynamics, thermalization, universality and dynamical phase transitions beyond traditional condensed matter paradigms. In addition to being theoretically appealing, these questions are strongly motivated by the rapid progress in ultra-cold atomic, molecular, and trapped ion systems that offer promising experimental platforms to investigate the dynamics of closed quantum systems. More generally, recent experimental advances in ultrafast optics and pump-probe spectroscopy, solid-state qubits, ultracold gases or quantum nanostructures have opened up exciting avenues for non-equilibrium quantum physics, with many open questions such as quantum transport beyond linear-response or the existence of novel dynamical phases of matter with no equilibrium counterparts. A central theme in my research is studying the non-equilibrium dynamics of low-dimensional strongly-correlated quantum systems, with some emphasis on entanglement spreading, quantum quenches, hydrodynamics and far-from-equilibrium transport.
Review articles:
- Nonequilibrium quantum dynamics and transport: from integrability to many-body localization, R. Vasseur and J.E. Moore, J. Stat. Mech. (2016) 064010.
- Hydrodynamics of weak integrability breaking, A. Bastianello, A. De Luca and R. Vasseur, J. Stat. Mech. (2021) 114003.
- JSTAT special issue on emergent hydrodynamics in integrable many-body systems: see here
- Anomalous transport from hot quasiparticles in interacting spin chains, S. Gopalakrishnan & R. Vasseur, Rep. Prog. Phys. 86 036502 (2023).
- Superdiffusion from nonabelian symmetries in nearly integrable systems, S. Gopalakrishnan & R. Vasseur, Annual Reviews of Condensed Matter Physics, Vol. 15:159-176 (2024).
Periodically driven (Floquet) quantum systems
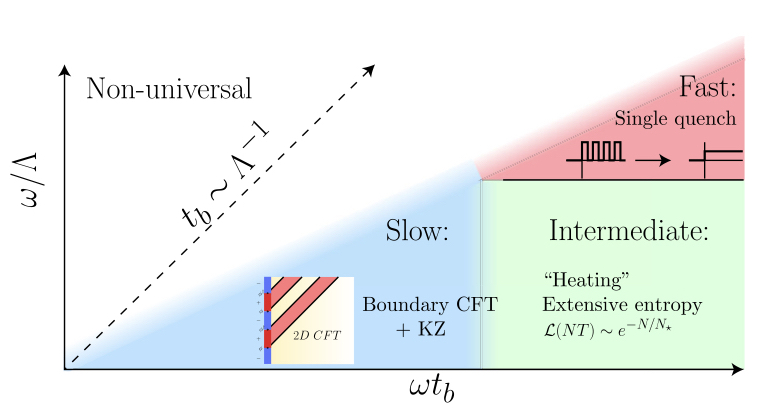 Recent years have witnessed substantial progress in understanding the dynamics of periodically driven (Floquet) systems. Low dimensional quantum critical systems are a natural setting in which to study Floquet dynamics, as many insights into the non-equilibrium dynamics of many-body systems have come from the study of Conformal Field Theories (CFTs) in 1+1d. Despite the naive expectation that such gapless systems should absorb energy and simply heat up when subjected to a boundary drive, we have identified distinct regimes in which the system shows universal features that can be understood using tools of field theory and scaling theory. Recently, I also studied the dynamical phase transitions separating distinct Floquet phases of matter by developing novel renormalization group techniques. We proposed a general picture of “Floquet quantum criticality” in terms of a distinct type of domain wall associated with time translational symmetry-breaking. Even more recently, we also uncovered a new class of “Thouless pumps” in interacting, translation-invariant Floquet systems, that are intrinsically-Floquet integrable systems with chiral (topologically non-trivial) quasiparticles.
Recent years have witnessed substantial progress in understanding the dynamics of periodically driven (Floquet) systems. Low dimensional quantum critical systems are a natural setting in which to study Floquet dynamics, as many insights into the non-equilibrium dynamics of many-body systems have come from the study of Conformal Field Theories (CFTs) in 1+1d. Despite the naive expectation that such gapless systems should absorb energy and simply heat up when subjected to a boundary drive, we have identified distinct regimes in which the system shows universal features that can be understood using tools of field theory and scaling theory. Recently, I also studied the dynamical phase transitions separating distinct Floquet phases of matter by developing novel renormalization group techniques. We proposed a general picture of “Floquet quantum criticality” in terms of a distinct type of domain wall associated with time translational symmetry-breaking. Even more recently, we also uncovered a new class of “Thouless pumps” in interacting, translation-invariant Floquet systems, that are intrinsically-Floquet integrable systems with chiral (topologically non-trivial) quasiparticles.
- Floquet Dynamics of Boundary-Driven Systems at Criticality, W. Berdanier, M. Kolodrubetz, R. Vasseur & J.E. Moore, Phys. Rev. Lett. 118, 260602 (2017).
- Floquet Quantum Criticality, W. Berdanier, M. Kolodrubetz, S.A. Parameswaran & R. Vasseur, .
- Strong-Disorder Renormalization Group for Periodically Driven Systems, William Berdanier, Michael Kolodrubetz, S. A. Parameswaran & Romain Vasseur, Phys. Rev B 98, 174203 (2018).
- Integrable Many-Body Quantum Floquet-Thouless Pumps, A.J. Friedman, S. Gopalakrishnan and R. Vasseur, Phys. Rev. Lett. 123, 170603 (2019).
- Fredkin Staircase: An Integrable System with a Finite-Frequency Drude peak, H. Singh, R. Vasseur & S. Gopalakrishnan, Phys. Rev. Lett. 130, 046001 (2023).
Anomalous transport in one-dimensional quantum magnets
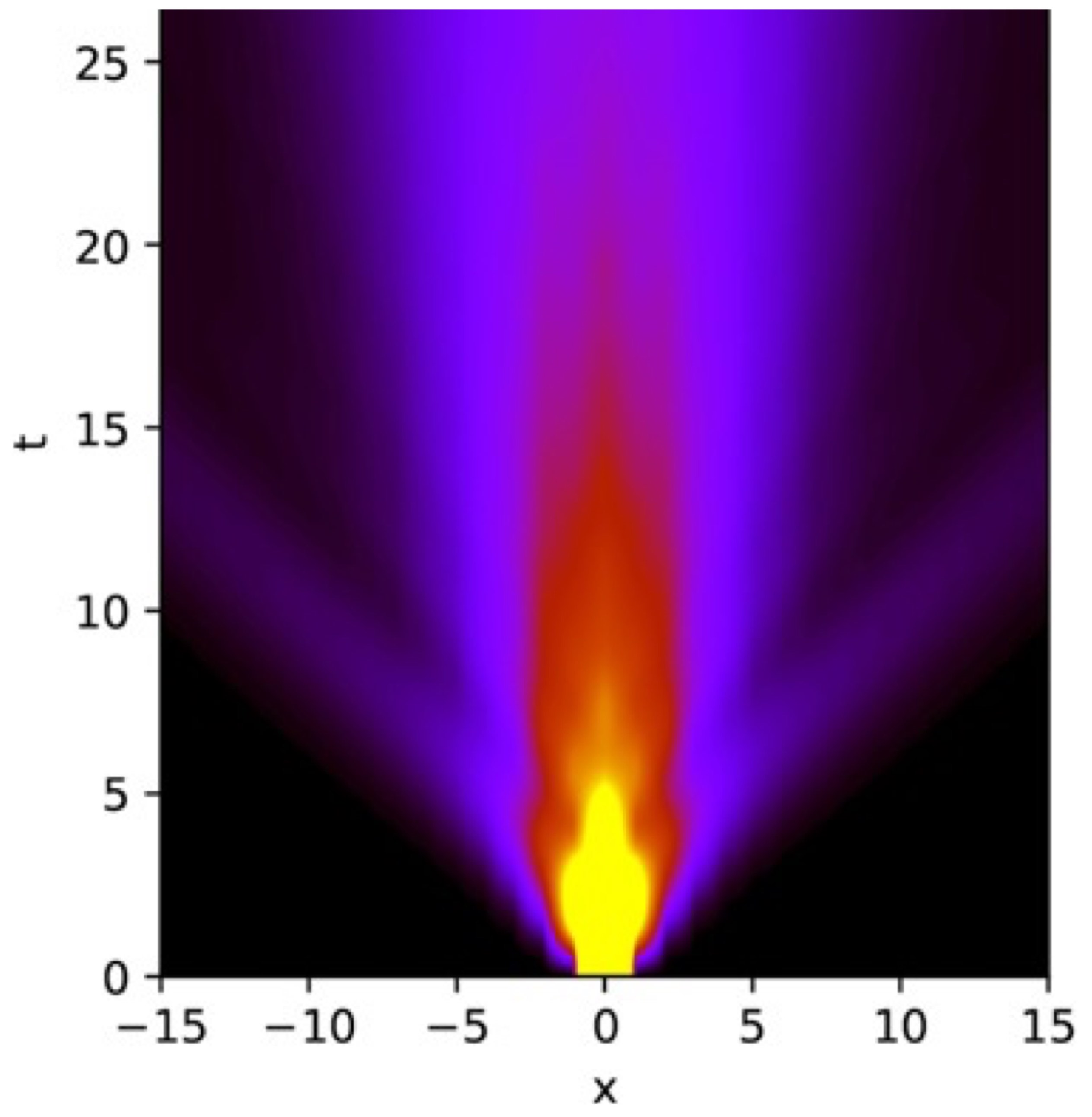 The XXZ model is a canonical model of quantum magnetism. In one dimension, this model is integrable and has ballistically moving quasiparticles. Thus, energy spreads ballistically, but, surprisingly, spin transport can be diffusive or superdiffusive. In collaboration with Sarang Gopalakrishnan, my group has worked on the theory of this anomalous transport using a kinetic picture based on generalized hydrodynamics and fluctuations. We computed the diffusion constant of the XXZ chain in the gapped regime at infinite temperature, and provided the first theoretical explanation for the anomalous dynamical exponent z=3/2 at the isotropic point — reminiscent of the KPZ (Kardar–Parisi–Zhang) universality class. As we showed recently, superdiffusive transport can be explained by the emergence of “soft” classical solitons and proposed a nonlinear fluctuating hydrodynamic theory for this KPZ scaling. We also studied spin transport in the presence of a small magnetic field, and uncovered a dynamical phase transition in this model, with a “phase” characterized by anomalous local spin relaxation. In easy-plane XXZ spin chains, we found that the spin conductivity diverges at low frequencies, but for special “commensurate” parameters it has a finite limit. These results explain longstanding puzzles regarding the discontinuous parameter dependence of the dc response. Superdiffusive transport is “superuniversal” in integrable systems with non-Abelian symmetries, and also occurs in the Hubbard model. This KPZ scaling was recently observed in neutron scattering experiments and in optical lattice Hubbard emulators.
The XXZ model is a canonical model of quantum magnetism. In one dimension, this model is integrable and has ballistically moving quasiparticles. Thus, energy spreads ballistically, but, surprisingly, spin transport can be diffusive or superdiffusive. In collaboration with Sarang Gopalakrishnan, my group has worked on the theory of this anomalous transport using a kinetic picture based on generalized hydrodynamics and fluctuations. We computed the diffusion constant of the XXZ chain in the gapped regime at infinite temperature, and provided the first theoretical explanation for the anomalous dynamical exponent z=3/2 at the isotropic point — reminiscent of the KPZ (Kardar–Parisi–Zhang) universality class. As we showed recently, superdiffusive transport can be explained by the emergence of “soft” classical solitons and proposed a nonlinear fluctuating hydrodynamic theory for this KPZ scaling. We also studied spin transport in the presence of a small magnetic field, and uncovered a dynamical phase transition in this model, with a “phase” characterized by anomalous local spin relaxation. In easy-plane XXZ spin chains, we found that the spin conductivity diverges at low frequencies, but for special “commensurate” parameters it has a finite limit. These results explain longstanding puzzles regarding the discontinuous parameter dependence of the dc response. Superdiffusive transport is “superuniversal” in integrable systems with non-Abelian symmetries, and also occurs in the Hubbard model. This KPZ scaling was recently observed in neutron scattering experiments and in optical lattice Hubbard emulators.
- Kinetic Theory of Spin Diffusion and Superdiffusion in XXZ Spin Chains, S. Gopalakrishnan and R. Vasseur, Phys. Rev. Lett. 122, 127202 (2019).
- Generalized hydrodynamics, quasiparticle diffusion, and anomalous local relaxation in random integrable spin chains, U. Agrawal, S. Gopalakrishnan and R. Vasseur, Phys. Rev. B 99, 174203 (2019).
- Anomalous relaxation and the high-temperature structure factor of XXZ spin chains, S. Gopalakrishnan, R. Vasseur, and B. Ware, PNAS 116 (33) 16250-16255 (2019).
- Anomalous low-frequency conductivity in easy-plane XXZ spin chains, U. Agrawal, S. Gopalakrishnan, R. Vasseur and B. Ware, Phys. Rev. B 101, 224415 (2020).
- Superdiffusion from emergent classical solitons in quantum spin chains, J. De Nardis, S. Gopalakrishnan, E. Ilievski and R. Vasseur, Phys. Rev. Lett. 125, 070601 (2020).
- Spin crossovers and superdiffusion in the one-dimensional Hubbard model, M. Fava, B. Ware, S. Gopalakrishnan, R. Vasseur and S. Parameswaran, Phys. Rev. B 102, 115121 (2020).
- Superuniversality of Superdiffusion, E. Ilievski, J. De Nardis, S. Gopalakrishnan, R. Vasseur, and B. Ware, Phys. Rev. X 11, 031023 (2021).
- Nonlinear fluctuating hydrodynamics for Kardar-Parisi-Zhang scaling in isotropic spin chains, Phys. Rev. Lett. 131, 197102 (2023).
- Tunable superdiffusion in integrable spin chains using correlated initial states, H. Singh, M. Kolodrubetz, S. Gopalakrishnan & R. Vasseur, Phys. Rev. Lett. 132, 176303 (2024).
Hydrodynamics of weak integrability breaking
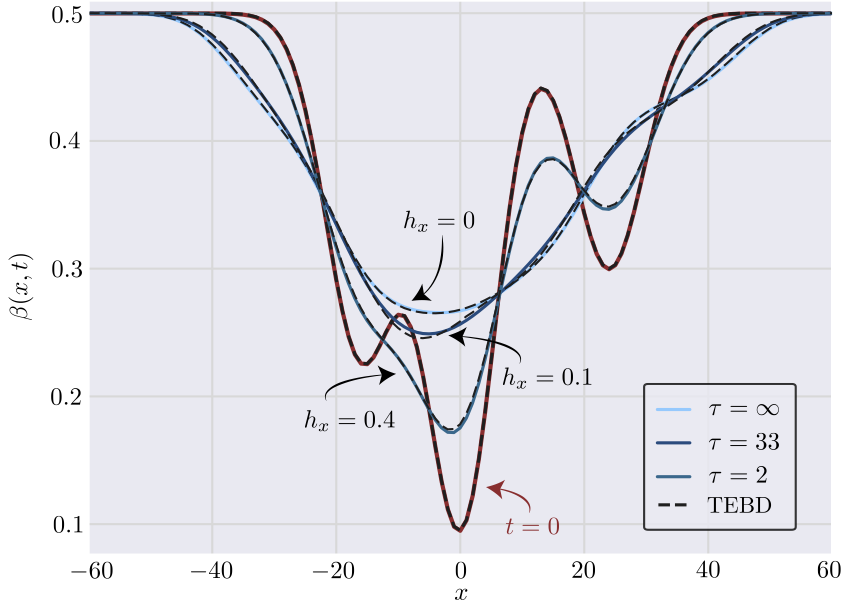 Integrable systems have infinitely many conserved quantities, which spread ballistically in general. When integrability is broken, only a few of these conserved quantities survive. The remaining conserved quantities are generically transported diffusively. My group, together with S. Gopalakrishnan, has recently proposed a hydrodynamical framework to describe this crossover between generalized to conventional hydrodynamics in nearly integrable systems. We’ve also proposed a generalized relaxation time approximation that turned out to be remarkably accurate to capture the crossover between ballistic and diffusive hydrodynamics in strongly-interacting systems close to integrability. Recently, we applied this formalism to show that superdiffusion is surprisingly robust to integrability breaking perturbations that respect non-Abelian symmetries. For quantum spin chains with large anisotropy, breaking integrability can even lead to a long-lived subdiffusive regime, leading to a diffusive regime with a non-perturbative diffusion constant at long times.
Integrable systems have infinitely many conserved quantities, which spread ballistically in general. When integrability is broken, only a few of these conserved quantities survive. The remaining conserved quantities are generically transported diffusively. My group, together with S. Gopalakrishnan, has recently proposed a hydrodynamical framework to describe this crossover between generalized to conventional hydrodynamics in nearly integrable systems. We’ve also proposed a generalized relaxation time approximation that turned out to be remarkably accurate to capture the crossover between ballistic and diffusive hydrodynamics in strongly-interacting systems close to integrability. Recently, we applied this formalism to show that superdiffusion is surprisingly robust to integrability breaking perturbations that respect non-Abelian symmetries. For quantum spin chains with large anisotropy, breaking integrability can even lead to a long-lived subdiffusive regime, leading to a diffusive regime with a non-perturbative diffusion constant at long times.
- Diffusive hydrodynamics from integrability breaking, Aaron J. Friedman, S. Gopalakrishnan and R. Vasseur, Phys. Rev. B 101, 180302(R) (2020).
- Hydrodynamics of nonintegrable systems from a relaxation-time approximation, J. Lopez-Piqueres, B. Ware, S. Gopalakrishnan and R. Vasseur, Phys. Rev. B 103, L060302 (2021).
- Stability of superdiffusion in nearly integrable spin chains, J. De Nardis, S. Gopalakrishnan, R. Vasseur, and B. Ware, Phys. Rev. Lett. 127, 057201 (2021).
- Integrability breaking in the Rule 54 cellular automaton, J, Lopez-Piqueres, S. Gopalakrishnan and R. Vasseur, J. Phys. A: Math. Theor. 55 234005 (2022).
- Subdiffusive hydrodynamics of nearly integrable anisotropic spin chains, J. De Nardis, S. Gopalakrishnan, R. Vasseur & B. Ware, Proceedings of the National Academy of Sciences 119 (34) e2202823119 (2022).
- Integrability breaking from backscattering, J. Lopez-Piqueres & R. Vasseur, Phys. Rev. Lett. 130, 247101 (2023).
Non-linear response Most conventional experimental probes of many-body systems, from spectroscopy to
 transport, operate in the linear-response regime. Despite its many successes, linear response has its limitations as a probe of correlated quantum matter. For example, many different mechanisms — of varying levels of interest — give rise to incoherent spectral continua, and cannot be differentiated on the basis of linear-response data. Recently, various experimental probes of nonlinear response have been developed, including pump-probe spectroscopy and multidimensional coherent spectroscopy in condensed-matter settings. Despite a flurry of recent work, the theoretical toolbox for addressing nonlinear response in generic interacting quantum many-body systems is primitive, with few exact results beyond free theories and those that reduce to ensembles of two-level systems. We have been working on developing new hydrodynamic and semi-classical approaches to study non-linear response functions in quantum spin chains (Ising chains and Heisenberg magnets in particular).
transport, operate in the linear-response regime. Despite its many successes, linear response has its limitations as a probe of correlated quantum matter. For example, many different mechanisms — of varying levels of interest — give rise to incoherent spectral continua, and cannot be differentiated on the basis of linear-response data. Recently, various experimental probes of nonlinear response have been developed, including pump-probe spectroscopy and multidimensional coherent spectroscopy in condensed-matter settings. Despite a flurry of recent work, the theoretical toolbox for addressing nonlinear response in generic interacting quantum many-body systems is primitive, with few exact results beyond free theories and those that reduce to ensembles of two-level systems. We have been working on developing new hydrodynamic and semi-classical approaches to study non-linear response functions in quantum spin chains (Ising chains and Heisenberg magnets in particular).
- Divergent nonlinear response from quasiparticle interactions, M. Fava, S. Gopalakrishnan, R. Vasseur, F. Eisler & S. Parameswaran, Phys. Rev. Lett. 131, 256505 (2023).
Fluctuations and full counting statistics
- Full counting statistics of charge in chaotic many-body quantum systems, E. McCulloch, J. De Nardis, S. Gopalakrishnan & R. Vasseur, Phys. Rev. Lett. 131, 210402 (2023).
- Distinct universality classes of diffusive transport from full counting statistics, S. Gopalakrishnan, A. Morningstar, R. Vasseur & V. Khemani, Phys. Rev. B 109, 024417 (2024).
Non-equilibrium steady-states and hydrodynamics

Quantum integrable systems, such as the interacting Bose gas in one dimension and the XXZ quantum spin chain, have an extensive number of local conserved quantities that endow them with exotic thermalization and transport properties. We studied numerically and analytically non-equilibrium steady states in such systems involving ballistic heat and spin currents, and showed that in some cases, they can be described using an emergent thermodynamic description. We also provided a general solution (both numerically and analytically) of the “Bethe-Boltzmann” hydrodynamic equations that describe the evolution in time of integrable quantum systems from local to global equilibrium. The solution of these kinetic equations allowed us to model experiments on ultracold one-dimensional Bose gases.
- Expansion potentials for exact far-from-equilibrium spreading of particles and energy, R. Vasseur, C. Karrasch and J.E. Moore, Phys. Rev. Lett. 115, 267201 (2015).
- Nonequilibrium quantum dynamics and transport: from integrability to many-body localization, R. Vasseur and J.E. Moore, J. Stat. Mech. (2016) 064010.
- Bethe-Boltzmann Hydrodynamics and Spin Transport in the XXZ spin chain, V.B. Bulchandani, R. Vasseur, C. Karrasch and J.E. Moore, Phys. Rev. B 97, 045407 (2018).
- Solvable Hydrodynamics of Quantum Integrable Systems, V.B. Bulchandani, R. Vasseur, C. Karrasch and J.E. Moore, Phys. Rev. Lett. 119, 220604 (2017).
- Hydrodynamics of operator spreading and quasiparticle diffusion in interacting integrable systems, Sarang Gopalakrishnan, David A. Huse, Vedika Khemani, and Romain Vasseur, Phys. Rev B 98, 220303(R) (2018).
- Hydrodynamic relaxation of spin helices, G. Cecile, S. Gopalakrishnan, R. Vasseur & J. De Nardis, Phys. Rev. B 108, 075135 (2023).
Quenching topological edge modes
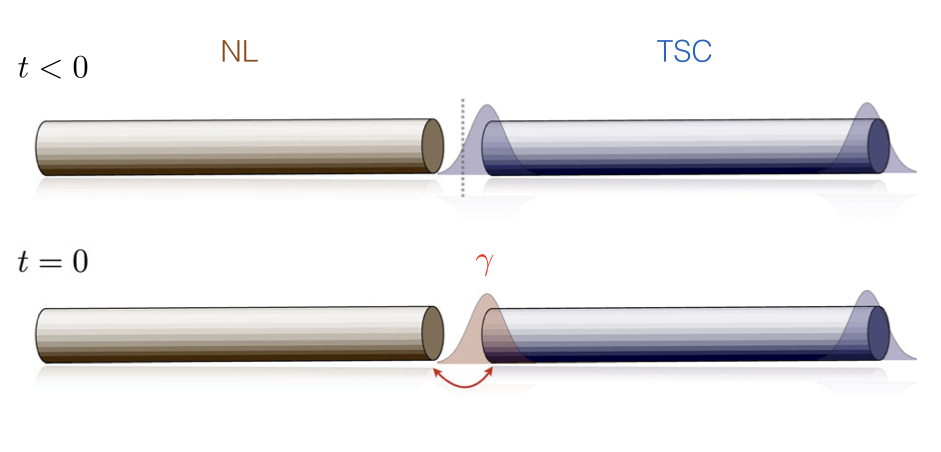 Quantum quenches – the abrupt change of a control parameter in a quantum system – provide a useful way to study the non-equilibrium physics of quantum systems and reveal the existence of new phenomena (dynamical transitions, non-thermal steady-states, prethermalization etc.). We are interested in finding new ways to probe the protected edge modes of topological insulators and superconductors using local quantum quenches, as an alternative to usual transport-based methods. The peculiar nature of topological edges leads to a remarkably robust universal post-quench dynamics, with clear non-equilibrium signatures that could be accessed in optical absorption experiments. This applies in particular to Majorana zero modes that emerge in certain types of topological superconducting materials. We found that the peculiar nature of Majorana zero modes leads to signatures in the dynamics following a quantum quench that are completely universal and robust against details of the setup.
Quantum quenches – the abrupt change of a control parameter in a quantum system – provide a useful way to study the non-equilibrium physics of quantum systems and reveal the existence of new phenomena (dynamical transitions, non-thermal steady-states, prethermalization etc.). We are interested in finding new ways to probe the protected edge modes of topological insulators and superconductors using local quantum quenches, as an alternative to usual transport-based methods. The peculiar nature of topological edges leads to a remarkably robust universal post-quench dynamics, with clear non-equilibrium signatures that could be accessed in optical absorption experiments. This applies in particular to Majorana zero modes that emerge in certain types of topological superconducting materials. We found that the peculiar nature of Majorana zero modes leads to signatures in the dynamics following a quantum quench that are completely universal and robust against details of the setup.
Local quantum quenches
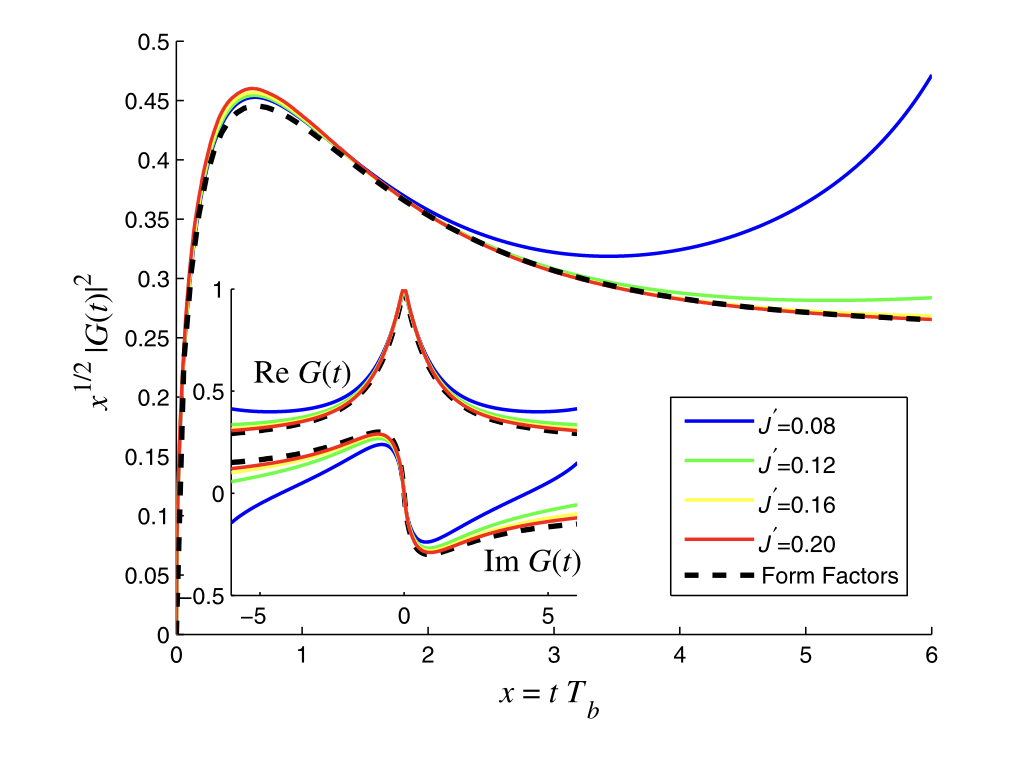
The study of two one-dimensional systems connected by some sort of interaction has become paradigmatic in modern quantum physics. It plays a particularly important role in the context of local quenches, transport through quantum dots, and the dynamics of magnetic impurities. An essential feature of these systems is the existence of crossover scales, which play a role similar to the Kondo temperature in the Kondo problem, and qualitatively separate weak and strong coupling regimes. Using the underlying integrability of such quantum impurity systems, we proposed new analytical techniques to study this dynamical crossover in non-equilibrium setups.
- Crossover physics in the non-equilibrium dynamics of quenched quantum impurity systems, Romain Vasseur, Kien Trinh, Stephan Haas and Hubert Saleur. Phys. Rev. Lett. 110, 240601 (2013).
- Universal quench dynamics of interacting quantum impurity systems, D.M. Kennes, V. Meden and R. Vasseur, Phys. Rev. B 90, 115101 (2014).
- Universal Entanglement Dynamics following a Local Quench, R. Vasseur and H. Saleur, SciPost Phys. 3, 001 (2017).