Many-body localization and Thermalization
The laws of thermodynamics can break down in disordered quantum systems that are isolated from external heat sources, due to the localization of excitations that would ordinarily transport energy among distant regions to establish thermal equilibrium. Such many-body localized (MBL) systems have the remarkable property that almost all high-energy excited states behave like zero-temperature quantum ground states. This raises the intriguing possibility that quantum coherent phenomena such as quantum and topological order or quantum criticality, typically associated with zero-temperature systems, can occur in arbitrarily “hot” matter. Cold atomic, molecular, and trapped ion systems offer a promising experimental platform to explore these theoretical ideas. Much of my recent work has been devoted to understanding the universal nature of the dynamics in the MBL phase and near the many-body delocalization transition to an ergodic state.
Review articles:
- Nonequilibrium quantum dynamics and transport: from integrability to many-body localization, R. Vasseur and J.E. Moore, J. Stat. Mech. (2016) 064010.
- Eigenstate phase transitions and the emergence of universal dynamics in highly excited states, S. A. Parameswaran, A.C. Potter & R. Vasseur, Annalen der Physik, 1600302 (2017).
- Many-body localization, symmetry and topology, S.A. Parameswaran and Romain Vasseur, 2018 Rep. Prog. Phys. 81, 082501.
See also our discussion of finite-size effects in MBL systems: Distinguishing localization from chaos: challenges in finite-size systems, D.A Abanin, J.H. Bardarson, G.De Tomasi, S. Gopalakrishnan, V. Khemani, S.A. Parameswaran, F. Pollmann, A.C. Potter, M. Serbyn and R. Vasseur, Annals of Physics 427,168415 (2021).
Theory of the many-body localization transition
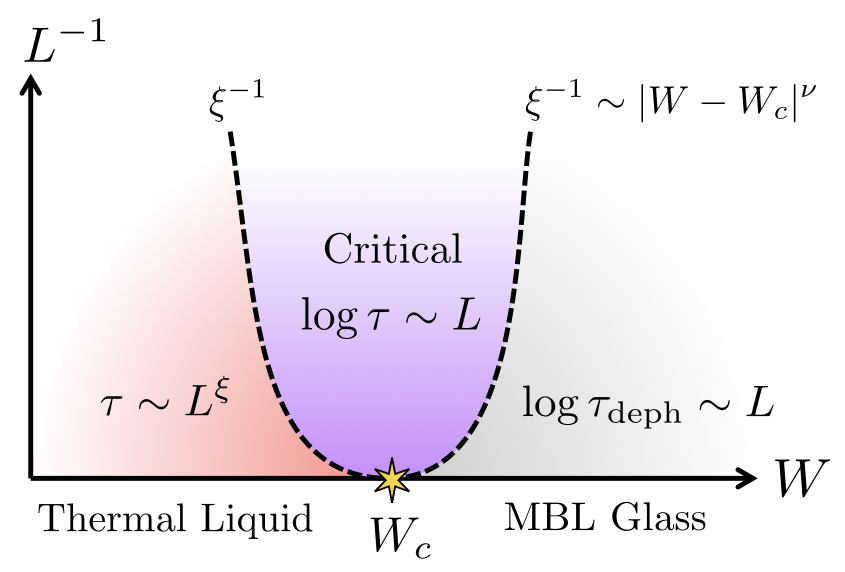 Excited states of interacting one-dimensional systems are many-body localized only at sufficiently strong disorder, and melt continuously into an ergodic, high temperature, classical liquid as disorder is weakened. In contrast to conventional classical or quantum phase transitions, this dynamical delocalization transition represents an entirely new type of critical point in which statistical mechanics and thermalization break down sharply at a continuous phase transition. We proposed a novel renormalization group approach to derive an effective quantum percolation model by accounting for collective resonant tunneling processes. This leads to a picture of delocalization driven via a percolating resonant backbone. In this way, we computed scaling properties of entanglement, dynamics, and energy transport and find an unusual critical structure that has no precedent in more conventional classical or quantum phase transitions. We proposed a scaling theory of entanglement near the transition, revealing some discontinuous aspects and a bimodal structure. Recently, we constructed a unifying picture of the MBL transition in one dimension in terms of a two-parameter Kosterlitz-Thouless scaling, relying on the fact that the transition is driven by `avalanches’. We showed that this simple picture is compatible with many different microscopically motivated RG models for the transition.
Excited states of interacting one-dimensional systems are many-body localized only at sufficiently strong disorder, and melt continuously into an ergodic, high temperature, classical liquid as disorder is weakened. In contrast to conventional classical or quantum phase transitions, this dynamical delocalization transition represents an entirely new type of critical point in which statistical mechanics and thermalization break down sharply at a continuous phase transition. We proposed a novel renormalization group approach to derive an effective quantum percolation model by accounting for collective resonant tunneling processes. This leads to a picture of delocalization driven via a percolating resonant backbone. In this way, we computed scaling properties of entanglement, dynamics, and energy transport and find an unusual critical structure that has no precedent in more conventional classical or quantum phase transitions. We proposed a scaling theory of entanglement near the transition, revealing some discontinuous aspects and a bimodal structure. Recently, we constructed a unifying picture of the MBL transition in one dimension in terms of a two-parameter Kosterlitz-Thouless scaling, relying on the fact that the transition is driven by `avalanches’. We showed that this simple picture is compatible with many different microscopically motivated RG models for the transition.
- Universal properties of many-body delocalization transitions, A.C. Potter, R. Vasseur and S.A. Parameswaran, Phys. Rev. X 5, 031033 (2015).
- Eigenstate phase transitions and the emergence of universal dynamics in highly excited states, S. A. Parameswaran, A.C. Potter & R. Vasseur, Annalen der Physik, 1600302 (2017).
- Scaling Theory of Entanglement at the Many-Body Localization Transition, Philipp T. Dumitrescu, Romain Vasseur and Andrew C. Potter, Phys. Rev. Lett. 119, 110604 (2017).
- Analytically solvable renormalization group for the many-body localization transition, Anna Goremykina, Romain Vasseur, and Maksym Serbyn, Phys. Rev. Lett. 122, 040601 (2019).
- Kosterlitz-Thouless scaling at many-body localization phase transition, Philipp Dumitrescu, Anna Goremykina, S. Parameswaran, M Serbyn, and R. Vasseur, Phys. Rev. B 99, 094205 (2019).
- Many-body localization transition with correlated disorder, Z.D. Shi, V. Khemani, R. Vasseur & S. Gopalakrishnan, Phys. Rev. B 106, 144201 (2022).
Quantum Critical Glasses
 The concepts of scaling and universality near a critical point are central to the modern understanding of equilibrium statistical mechanics and condensed matter physics. Using a quantitative and analytically tractable renormalization group method, we showed that universality and quantum criticality can also emerge at “infinite temperature”, far from thermal equilibrium. Our approach provides us with an infinite family of systems whose excited states exhibit properties characteristic of quantum critical ground states. These “quantum critical glasses” can therefore be thought of as critical variants of MBL, and represent an entirely new class of non-equilibrium dynamical phases and phase-transitions with no equilibrium counterparts.
The concepts of scaling and universality near a critical point are central to the modern understanding of equilibrium statistical mechanics and condensed matter physics. Using a quantitative and analytically tractable renormalization group method, we showed that universality and quantum criticality can also emerge at “infinite temperature”, far from thermal equilibrium. Our approach provides us with an infinite family of systems whose excited states exhibit properties characteristic of quantum critical ground states. These “quantum critical glasses” can therefore be thought of as critical variants of MBL, and represent an entirely new class of non-equilibrium dynamical phases and phase-transitions with no equilibrium counterparts.
- Quantum criticality of hot random spin chains, R. Vasseur, A.C. Potter and S.A. Parameswaran, Phys. Rev. Lett. 114, 217201 (2015).
- Universal crossover from ground state to excited-state criticality, B. Kang, A.C. Potter and R. Vasseur, Phys. Rev. B 95, 024205 (2017).
- Eigenstate phase transitions and the emergence of universal dynamics in highly excited states, S. A. Parameswaran, A.C. Potter & R. Vasseur, Annalen der Physik, 1600302 (2017).
Many-body localization and Symmetries
The concept of symmetry plays a crucial role in our understanding of phases of matter. The interplay of symmetry and dimensionality leads to very general constraints on possible types of symmetry-breaking phases and phase transitions, such as the Peierls or Mermin-Wagner theorems. We derived similar constraints for quantum systems far-from-equilibrium, and showed that MBL is not possible with symmetry groups that protect multiplets (e.g., all non-Abelian symmetry groups). Our results rule out the existence of many MBL symmetry-protected topological phases including electronic topological insulators. We investigated the consequences of this no-go theorem for random-bond XXZ spin chains, and for the protection of topological parafermionic zero modes using MBL. More recently, we also analyzed the instability of tentative nonergodic phases in non-Abelian quantum chains, and derived expressions for the thermalization timescales and length scales.
- Particle-hole symmetry, many-body localization, and topological edge modes, R. Vasseur, A.J. Friedman, S.A. Parameswaran and A.C. Potter, Phys. Rev. B 93, 134207 (2016).
- Symmetry constraints on many-body localization, A.C. Potter and R. Vasseur, Phys. Rev. B 94, 224206 (2016).
- Localization-protected order in spin chains with non-Abelian discrete symmetries, A.J. Friedman, R. Vasseur, A.C. Potter and S. A. Parameswaran, Phys. Rev. B 98, 064203 (2018).
- Perturbative instability of nonergodic phases in non-Abelian quantum chains, B. Ware, D. Abanin, and R. Vasseur, Phys. Rev. B 103, 094203 (2021).
Properties of the many-body localized phase
 Much of our understanding of the MBL phase relies on diagnostics very difficult to access experimentally, such as entanglement or level statistics. We have argued that the dephasing mechanism underlying the logarithmic entanglement growth characteristic of MBL is also responsible for the strong suppression of quantum revivals of local observables in the many-body localized phase. This is the first single-spin probe of MBL that is capable of distinguishing between ergodic, many-body localized, and non-interacting Anderson localized phases, and it is anticipated that experiments may soon be in a regime where such an analysis is feasible. The figure shows the revival rate as a function of time for different interaction strengths.
Much of our understanding of the MBL phase relies on diagnostics very difficult to access experimentally, such as entanglement or level statistics. We have argued that the dephasing mechanism underlying the logarithmic entanglement growth characteristic of MBL is also responsible for the strong suppression of quantum revivals of local observables in the many-body localized phase. This is the first single-spin probe of MBL that is capable of distinguishing between ergodic, many-body localized, and non-interacting Anderson localized phases, and it is anticipated that experiments may soon be in a regime where such an analysis is feasible. The figure shows the revival rate as a function of time for different interaction strengths.