Computational Physics in Python
Python is an easy-to-learn and powerful programming language for computational physics. Here you can find some handouts on scientific programming in Python developed for the course Physics 281, Computational Physics.
Quantum computing
While it is difficult to build a real quantum computer it’s fun and easy to simulate one on a classical computer. We’ve done these projects as an add-on to a junior level quantum course, but the quantum mechanics background needed is not that much. Here is some Sample code for these projects.
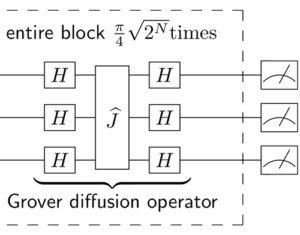Handout Part 1: Qubits and their measurement, Hadamard and phase-shift gates, Grover’s quantum search algorithm, CNOT gates.
Handout Part 2: Increasing the number of qubits, Shor’s quantum factoring algorithm. Most of Parts 1 and 2 are also in the article AJP 83, 688 (2015).
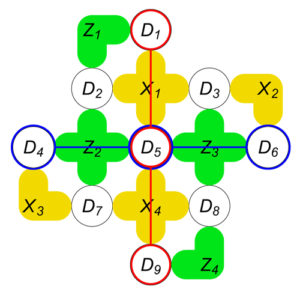Handout Part 3: Quantum error correction, quantum error codes, threshold theorem, the surface code, magic states and their distillation.
Quantized conductance
An ideal one-dimensional wire has the universal conductance (1/resistance) value 2e2/h = 1/(13 k?), and nano-sized wires tend to have conductances that are multiples of this value. This “quantization” of conductance in very tiny wires is easily demonstrated in a table-top experiment, see Nanocontacts talk and AJP 67, 389 (1999). You can also download a rather old LabView program and its documentation.
Bessel’s pendulum
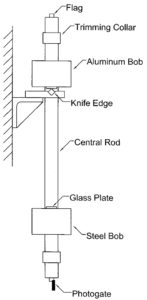In the 19th century the best way to measure the acceleration of gravity g was to use a carefully constructed pendulum. In 1826 Friedrich Bessel showed that an invertible (Kater) pendulum that was symmetric in shape but asymmetric in mass distribution would eliminate errors due to air drag and buoyancy. This makes a nice junior-level lab experiment, see AJP 69, 714 (2001).