Baseline correction is essential for T1, T2 and diffusion experiments as our target peaks are often broad and short, so any baseline imperfection can cause large errors.
Baseline correction is done by computer fitting of the baseline by a fifth order polynomial: y = A + Bx + Cx2 + Dx3 +Ex4 + Fx5. Since the baseline shapes cannot always be perfectly fit by such a polynomial and sometimes some peaks are so broad that the computer is having a hard time decide whether it is a peak or part of the baseline, we need to be aware of the limitations of the fitting algorithm and tweak strategy if the correction result is not good.
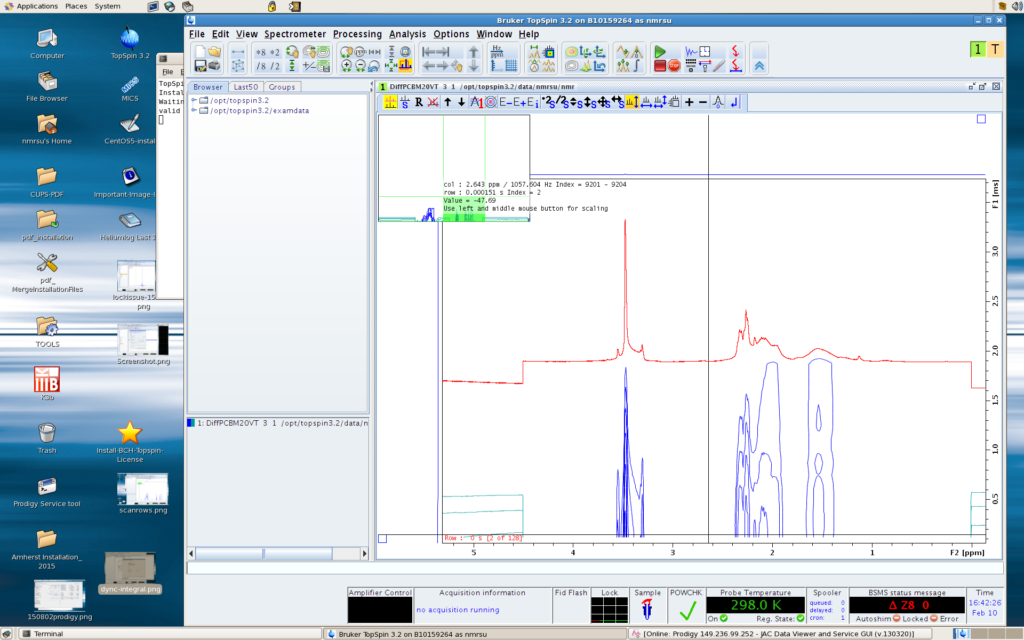
To check if your slices have good baselines, go to the Multiple Display mode. Make the peaks very tall so you can see the baseline well. When you do Scan Rows, zero intensity of each spectrum is at the middle line of the window. This means that a good baseline would not shift downward or upward if you adjust peak heights (remember: ten times zero is zero!). If, when you left click to make the peaks taller, the baseline sinks or rises, the baseline is not good and needs correction. Note that the vertical scale is erroneous – zero intensity of a slice is at the middle line of the window, while the 0 as indicated by the scale is at the bottom of the window.
While in the Multiple Display mode, you need to decide two factors for baseline correction: (1) a chemical shift range of spectrum in which you want baseline correction. Since it is often difficult to perfectly correct baseline across the entire spectrum, only correcting a smaller range often produces better result. For this, you will need to properly choose the left and right limit of the range that you want the baseline correction be done. Choose the limits such that tails of peaks do not extend there, i.e., there is only baseline or noise near there. In the figure below, I chose the limits to be 4.5 and 0 ppm. Write your choices down for the next step. (2) shape of the polynomial. I often find that lower orders of polynomial (linear, which means I only use the shape A + Bx; or quadratic, which means I only use the shape A + Bx + Cx2) do a better job than the ones that use all five orders, which often overdo the job.
Exit Multiple Display mode.
Click the tab ProcBars (on top row of the spectrum window). In Baseline Correction category, set ABSG to 1. This means that you allow the computer to fit the baseline with only a linear function (A + Bx), not the entire five orders of polynomial. I found this usually produces good result. Sometimes 2 is better. Experiment with it yourself. Set ABSF1 and ABSF2 to the left and right limits of your choice. Do this only for F2 dimension. F1 dimension is not used.
Click the Spectrum tab. On the command line, type abs2. This will perform an automatic baseline correction in the range of spectrum that you chose. Go back to Multiple Display and check the slices. It should look like the figure below. Note that the baseline of the spectrum between 4.5 and 0 ppm has been corrected. There are step changes at 4.5 and 0 ppm, which is because the spectrum within the window has been corrected for baseline and that outside the window still has very negative baseline. This is normal.
If you don’t like the correction result, just type xf2 again. This will erase all the baseline corrections that you have done. Start fresh from here.