Conventional wisdom (and testimonials from researchers who have been burned) says that time of day can introduce bias into crowdsourced data collection. Right now, SurveyMan posts a single HIT per survey, requesting $$n$$ assignments. If we collect $$n$$ assignments and find that they are low quality, we ask for more by extending the HIT.
What happens if we get $$n$$ valid responses in the first hour of posting? Is the distribution of responses going to be the same as if we had posted $$n$$ hits, distributed throughout the day? If I am posting surveys about American politics, I will want have them available when the largest number of American Turkers are active. However, if I am asking for annotations, do I need to be conscious of potential differences? The question of bias is insidious because we don’t know precisely when it applies. Andrew Mao has written about scheduling tasks during peak AMT worker hours. However, there’s still a lot domain knowledge and planning involved. Planning properly requires constant vigilance, since it’s not even clear that peak worker hours will remain the same over time: a recent paper found that the alleged biases in the mechanical turk population had either sorted themselves out or had been overstated. Conversely, Ipierotis et al. established an AMT demographic tracker, which can help identify subtle population biases.
Regardless of whether or not biases exist, most machine learning models that use AMT data account for this in some way. There is typically some unknown bias term drawn from a reasonably well-behaved distribution that can then be marginalized. When demographers and pollsters tackle this issue, they typically know something about the underlying population and account for uneven sampling with this prior information. However, when we don’t know anything about what the underlying population is supposed to look like, or if we have little prior information for our variables of interest, we may be in a bit of a bind.
Toward automatic detection of population differences
As an alternative to these approaches, I am implementing a prototype scheduler in SurveyMan that dynamically tests for biases. Let’s start with the basic assumption that there are no biases in data collection and that people answer our HITs within an hour of our posting. Since we cannot be sure of our assumption, we post a HIT with $$n/2$$ assignments at $$t_0$$ and $$n/2$$ assignments at $$t_{12}$$, where the subscripts indicate hours from the start of data collection. We schedule these two batches 12 hours apart in an attempt to get a kind of maximum difference in populations: as the researcher, if I am kicking off a survey at this time, chances are people who share demographic features to me will also be awake and working when I am working. However, 12 hours from now, I expect to be asleep and it might happen that the people who are taking my survey are quite different.
First challenge: how do we even tell if there are differences in the survey responses?
Approach 1: Check for differences in the distributions observed for each question.
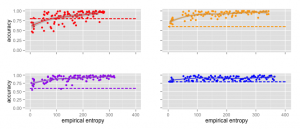
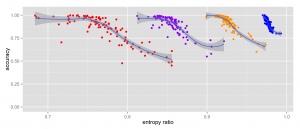
We look at the responses generated for a set of questions at two different times and calculate whether the distributions are significantly different. Since we will probably end up with a bunch of low-powered comparisons, we are likely to detect a difference. However, since we know the number of questions we’ll ask (and therefore the number of comparisons we’ll make) a priori, we should be able to model our false positive rate.
How many questions must be different for us to consider the populations fundamentally different? What happens if we find a significant difference between the responses for a particular question, but this question doesn’t have an impact on the analyses we might do? For example, suppose that we find different responses for a control question, but no difference in the questions of interest. Should we run the survey again?
Maybe one way of thinking about this approach is that it’s like an AutoMan approach, but in batch mode. I like to tell people that the way we came up with the idea for SurveyMan started out as a way to deal with batches of AutoMan tasks that converged to a distribution, rather than a point. Looking for individual differences in questions is a related problem, but it doesn’t really leverage running things in batch.
Approach 2: Look for differences in correlations.
For small numbers of questions, differences in distributions may suffice, but for a more complex survey, a more informative measure might be to look for differences in correlations between questions. This may do a better job of highlighting “important” differences in populations. Since it is very unlikely that we would find correlation coefficients that are exactly the same, we would need to be careful about how we might compare discovered correlations. How much variation should we expect? What’s our baseline? Zero correlation seems silly; is there a more meaningful baseline? Surely the baseline would depend on the survey itself.
If we expect there to be fluctuations in the demographics of AMT workers, why don’t we just post our surveys in slow progression — maybe one per hour? In addition to the troubles caused by the underlying AMT system (we get a boost when we first post; after a certain amount of time, engagement tapers off), we waste time doing this. It also isn’t clear what the scale of variation is — should we post over the course of a day, a week, a month, or a year? Some AMT demographic surveys run for at least one year. Clearly this is infeasible for many other types of research (e.g., the work we’d been doing with the linguists).